2(22)2019

Maria Mikos1

Zasięg dyfuzji bodźców gospodarczych – testowanie modelu rdzeń–peryferia w odniesieniu do kohezyjnej polityki regionalnej i lokalnej

Streszczenie

Dążenie do spójności stanowi podstawę polityki regionalnej Unii Europejskiej. Kolejne edycje strategii rozwojowych różnią się jednak między sobą obszarami koncentracji inwestycji. W pracy dokonano przeglądu teoretycznych modeli polityki regionalnej oraz określono główne obszary zainteresowania kolejnych strategii spójnościowych na przykładzie Polski. Za pomocą ekonometrycznego modelu interakcji przestrzennych wyznaczono przestrzenny zasięg dyfuzji bodźców rozwojowych z centrów na peryferia. Dynamiczna analiza danych dla lat 1996–2017 pozwoliła na empiryczną ocenę realizacji strategii rozwojowych w Polsce, a jej wyniki potwierdziła analiza L-momentów rozkładu przedsiębiorczości. Wyznaczono okres najwyższej skuteczności polityki spójności. Podjęto również próbę wytypowania obszarów odpowiedzialnych za brak skuteczności polityki opartej na metodologii smart.

Słowa kluczowe: polityka spójności, dyfuzja bodźców, rdzeń–peryferia

DOI: 10.33119/KSzPP/2019.2.3

Spatial range of the diffusion of economic incentives: testing the core–pheriphery model in reference to the regional and local cohesion policy

Abstract

The main goal of the EU regional policy is obtaining cohesion. However, development strategies differ in terms of investment concentration. The paper presents the theoretical models of the regional policy, illustrated with a case study of Polish strategies. Using the spatial interactions model, the range of the diffusion of economic incentives was estimated. A dynamic analysis of 1996–2017 NUTS4 panel data enabled the assessment of the results of development strategies. The outcome was confirmed with the L-moments analysis of entrepreneurship distribution over time. The method covered the period of the highest efficiency of the cohesion policy. The author also made an attempt to mark out factors responsible for the failure of the smart policy in Poland.

Keywords: cohesion policy, diffusion, core-periphery

Skuteczna polityka gospodarcza stanowi podstawę rozwoju państwa. Odgrywa szczególnie istotną rolę w walce z nierównościami oraz wspieraniu przedsiębiorczości. W Polsce, jak i w Europie, począwszy od lat 90. ubiegłego wieku, coraz większym zainteresowaniem cieszył się nurt „terytorialny”. Polityka ekonomiczna zaczęła być mocniej skoncentrowana na potrzebach konkretnych regionów (Herbut et al., 2007). Wraz z upływem czasu zmieniały się wizje prowadzenia polityki terytorialnej. Jednak najważniejszy wpływ na ich kształtowanie w Polsce miało przygotowanie do członkostwa, a następnie przystąpienie do Unii Europejskiej. Już przed akcesją polskie strategie rozwojowe były inspirowane działaniami zachodnimi, a po roku 2004 ich główne cele stały się niemal całkowicie zbieżne z proponowanymi przez Komisję Europejską.

Polityka regionalna Unii Europejskiej od początku koncentrowała się na nadrzędnym celu: osiągnięciu harmonijnego rozwoju, przy jednoczesnym niwelowaniu różnic międzyregionalnych i pogłębieniu integracji europejskiej (Hooghe, 1996). Również wykorzystywane metody (instrumenty finansowe oraz działania legislacyjne) nie uległy zmianie. Jednak w każdej kolejnej strategii rozwojowej w nieco inny sposób rozkładano akcenty, starając się coraz skuteczniej dążyć do spójności (Greta, Tomczak-Woźniak, 2014).

Po dwóch dekadach prowadzenia świadomej polityki regionalnej w Polsce według różnych planów warto się zastanowić, który z nich przynosił najlepsze rezultaty. Jest to dobry moment, aby przyjrzeć się rzeczywistym wzorcom dyfuzji rozwoju wewnątrz kraju oraz zastanowić się, jak głębokie jest zjawisko peryferyjności. Ze względu na to, że spójność jest bardzo szerokim pojęciem, wymykającym się tradycyjnym definicjom, należy opracować metodę, która pozwoliłaby na oszacowanie wpływu stosowanych strategii na podstawie danych empirycznych.

Polityka gospodarcza ostatnich dwóch dekad może być analizowana przez pryzmat trzech modeli teoretycznych, które stanowiły podstawę do budowania europejskiej polityki regionalnej. Po pierwsze, jest to klasyczny model rdzenia–peryferii, który dał podstawy dla innej koncepcji – inwestowania w „motory wzrostu”. Trzecim podejściem jest nowoczesna adaptacja tej myśli – model rozwoju inteligentnego (smart growth), który stoi u podstaw obecnie obowiązującej strategii Europa 2020. Osią tych modeli jest pojęcie spójności. Operacjonalizacja tych modeli jest możliwa przy wykorzystaniu rodziny modeli interakcji przestrzennych.

Celem pracy jest przedstawienie wyników empirycznych badania zasięgu dyfuzji bodźców rozwojowych z centrów wojewódzkich. Pomiary dotyczą lat 1996–2017, a więc okresu prowadzenia przez Polskę intensywnej polityki regionalnej. Uzyskane estymacje modelu oraz wyniki metody L-momentów służą za podstawę oceny skuteczności stosowanych strategii i ich przełożenia na rzeczywiste efekty dążenia do uzyskania spójności jednostkowej. Wykorzystane do badania dane pochodzą z Głównego Urzędu Statystycznego, a proces modelowania został przeprowadzony przy wykorzystaniu oprogramowania R w wersji 3.5.1.

Teoretyczne modele kształtowania polityki regionalnej

Model rdzenia–peryferii (core–periphery model) jest podstawą większości teorii rozwoju regionalnego. Jego główne założenia można znaleźć w książce J. Friedmanna z 1967 r. Opiera się on na prostym modelu polaryzacyjnym, spójnym z wcześniejszymi pracami F. Perroux (1964) oraz A. O. Hirschmana (1958). Występują w nim dwa podstawowe elementy: centrum – lokalizacje wyposażone w kapitał, siłę finansową, ośrodki badawcze i przemysłowe oraz przedsiębiorcze elity społeczne; a także peryferia – obszary bogate w siłę roboczą i surowce, mało rozwinięte, wydrenowane z wykształconych elit (Friedmann, 1967). Między jednym i drugim ośrodkiem następuje ciągła wymiana (Friedmann, 1967; Grzeszczak, 1999). W ujęciu klasycznym polega ona głównie na przepływie czynników produkcji, wyrobów gotowych i wynagrodzeń (Friedmann, 1967; Fujita et al. 2001). Inne prace rozszerzają to podejście o przepływ usług, innowacji oraz wykształconych pracowników – drenaż mózgów (Hryniewicz et al., 1997; Jałowiecki, Gorzelak, 2004; Pike et al., 2016).

W literaturze zwraca się również uwagę na niematerialne oddziaływanie centrów (Grzeszczak, 1999; Pike et al., 2016). Dzięki sile wytwórczej i nieustannemu dążeniu do rozwoju stanowią one motor wzrostu dla otaczających je obszarów (Friedmann, 1967). Interakcja międzyregionalna nie kończy się na przepływie kapitału, ale prowadzi również do dyfuzji technologii i wzrostu (Hirschman, 1958). Efekt oddziaływania Hirschmana (trickle-down effect) podlegał jednak krytyce, m.in. A. Glasmeier (2000) zwracała uwagę na trudności związane z odbieraniem sygnałów przez szczególnie niedorozwinięte peryferia. Ich specyfika i braki w lokalnej infrastrukturze nie pozwalają na korzystanie z pozytywnego wpływu centrum (Glasmeier, 2000). Inne prace akcentują również silne procesy dywergencyjne spowodowane intensywną wymianą między centrum a peryferiami (Lipshitz, 1992; Pike et al., 2016). Kosztem dynamicznego rozwoju rdzenia jest drenowanie okolicznych terytoriów z zasobów i odciąganie od nich możliwości rozwojowych (Hryniewicz, et al. 1997; Pike et al., 2016).

Głównym ograniczeniem w modelu jest możliwość przepływu ludzi i informacji między regionami. Jeśli siatka komunikacyjna jest słabo rozwinięta, wymiana między obszarami nie zachodzi, a synergiczne efekty rozwojowe nie występują (Friedmann, 1967). Model ten jest jednak na tyle uniwersalny, że można go zastosować zarówno w skali lokalnej (miasto–wieś), jak i międzynarodowej (wysoko rozwinięte państwa–obszary rozwijające się) (Fujita et al., 2001). Stanowi on również podstawę myślenia o rozwoju regionalnym.

Naturalnym rozwinięciem modelu rdzenia–peryferii jest koncepcja inwestowania w lokomotywy rozwoju. Powstała ona niejako z połączenia poprzedniego podejścia z ideą pozytywnych efektów zewnętrznych. Już J. Jacobs (1969) zwracała uwagę na to, że koncentracja aktywności ekonomicznej w dużych miastach sprzyja wymianie wiedzy między przedsiębiorcami i pracownikami. Zachodzące między aktorami interakcje nie tylko generują kapitał ludzki, ale również prowadzą do powstawania „masy krytycznej”, która znacząco poszerza możliwości produkcyjne i powoduje rosnące korzyści skali (Azariadis, Drazen, 1990).

Najistotniejszym elementem w tym podejściu jest jednak generowanie pozytywnych efektów zewnętrznych (Acemoglu, 2012). W procesie interakcji między aktorami dokonuje się nieliniowy wzrost produktywności, a powstały kapitał ludzki i innowacje technologiczne oddziałują na kolejnych uczestników procesu gospodarczego w wyniku dyfuzji (Acemoglu, 2012). Dzięki temu zjawisku rozwój z centrum może być transferowany do okolicznych terytoriów, a jak wykazano w literaturze, właśnie dyfuzja pozytywnych bodźców technologicznych stanowi napęd rozwoju sąsiedzkich regionów (Lucas, 1988; Azariadis, Drazen, 1990; Hauser, 2001; Acemoglu, 2012).

Taka koncepcja teoretyczna jest niezwykle zachęcająca z punktu widzenia polityki regionalnej – prowadzi bowiem do prostych i łatwych w zastosowaniu konkluzji. Jeśli najlepsze warunki do wzrostu znajdują się w metropoliach, a dzięki efektom zewnętrznym i dyfuzji rozwój samoistnie zostanie przetransferowany do okolicznych regionów (Hauser, 2001) – należy skoncentrować się na finansowaniu centrów (Szlachta, 2011). Dodatkowo, koncentracja środków w jednym obszarze pozwoli uniknąć problemu wyboru optymalnego rozdysponowania funduszy, a występujące w centrum korzyści skali doprowadzą do najbardziej efektywnego wykorzystania inwestycji.

Ograniczeniem tego podejścia jest jednak tzw. pułapka niedorozwoju (under­development trap). Przekazywane efekty zewnętrzne mogą się nie przyjąć, jeśli w docelowym środowisku występują braki w wykształceniu lub bazowy poziom kapitału ludzkiego jest zbyt niski (Azariadis, Drazen, 1990). W literaturze znajdują się również głosy krytyczne, które wykazują brak potwierdzenia w danych „zbawczej roli lokomotyw wzrostu”, szczególnie w kontekście dążenia do rozwoju zrównoważonego (Cesarski, 2013). Zwolennicy tej teorii mówią jednak, że finansowanie obszarów mniej rozwiniętych jest „marnotrawstwem ograniczonych środków publicznych”, a najlepszą drogą do uzyskania konkurencyjności i rozwoju państwa jest wykorzystanie potencjału centrów (Szlachta, 2011).

Model rozwoju inteligentnego (smart) jest nowoczesnym podejściem, koncentrującym się na naturalnym potencjale regionu (Foray et al., 2013). Według jego twórcy, najlepszym sposobem na wzrost jest aktywizacja terytorium w ramach jego dotychczasowych obszarów sukcesu (Foray, 2014). Nie oznacza to jednak ciągłego powtarzania tych samych strategii biznesowych. Rozwój smart ma prowadzić do odnajdywania nowych możliwości i tworzenia innowacji, zbliżonych i spójnych z pierwotną specjalizacją (Foray, 2014). Takie działanie prowadzi do dywersyfikacji możliwości produkcyjnych, uodpornienia na szoki zewnętrzne i nieustannego pobudzania do zmian zgodnych z trendami ekonomicznymi (Foray, 2014; McCann, Ortega-Argilés, 2011).

Inni badacze odnosili model smart do struktury rdzeni–peryferii (Camagni, Capello, 2013; McCann, Ortega-Argilés, 2011). W tym podejściu centrum jest obszarem o wysokim potencjale badawczym, kreującym nowe technologie (obszar B+R). Peryferia mają zaś odkryć swoją domenę wiedzy, osadzoną (embeddedness) w występujących już lokalnie umiejętnościach, wiedzy i kapitale ludzkim (McCann, Ortega-Argilés, 2011). Dzięki wyspecjalizowaniu się w niej, mogą rozpocząć skuteczną wymianę wiedzy, stosując w praktyce „przygotowane” w centrum innowacje (Camagni, Capello, 2013; McCann, Ortega-Argilés, 2011). Łączność (connectedness) między aktorami jest dwukierunkowa (McCann, Ortega-Argilés, 2011): peryferia komunikują się z centrum jako źródłem innowacji (zdatnych do wykorzystania w danym regionie zgodnie z jego specjalizacją); podejmują również wymianę z innymi obszarami peryferyjnymi, które rozwijają się w innych dziedzinach wiedzy (McCann, Ortega-Argilés, 2011). Ten drugi kierunek wspomaga integrację, wspiera proces wzajemnego uczenia się oraz stymuluje do nieustannego rozwoju i poszukiwania nowych nisz w ramach danej „domeny wiedzy” (Camagni, Capello, 2013).

Korzystny system wymiany wiedzy i synergii między centrum a peryferiami jest możliwy tylko dzięki zaangażowaniu lokalnych elit (Camagni, Capello, 2013). W tym podejściu są one definiowane jako przedsiębiorcy, osoby kreatywne i włączone w proces efektywnego gospodarowania dostępnymi zasobami (Camagni, Capello, 2013). To właśnie one powinny określać potrzeby i specjalizację regionu, sugerować obszary wymagające wsparcia oraz wskazywać kierunek dla lokalnej polityki. Brak przedsiębiorczych elit na danym obszarze lub brak ich zaangażowania w proces kształtowania strategii rozwojowych oraz problemy z łącznością z centrum stanowią główne ograniczenia w tym modelu (Capello, Kroll, 2016).

Powiązanie przedsiębiorstwa i przestrzeni – wpływ na rozwój firmy oraz otoczenia

Podstawowym elementem gospodarki rynkowej jest przedsiębiorstwo. To podejście wywodzi się już z dorobku ojca ekonomii – Adama Smitha (Rothschild, 1994). Klasycznie firmy postrzegano jako wehikuły służące do generowania zysku i pozyskiwania maksymalnej nadwyżki ekonomicznej (Giddens, 2000). Współcześnie częściej widzi się je jako podmioty wyposażone w niezbędne narzędzia do tworzenia innowacji, poszukiwania nowych możliwości i nie tylko dążące do rozwoju własnego, ale również prowadzące do wzrostu otoczenia (Giddens, 2000; Holtz-Eakin, 2000). Uważa się, że sami przedsiębiorcy bardzo silnie oddziałują na środowisko, w którym prowadzą swoją aktywność. Wymienia się tutaj ich skłonność do podejmowania powszechnie niechcianego ryzyka, szczególną kreatywność i zdolność do tworzenia energii ekonomicznej (Giddens, 2000; Littunen, 2000). Ta ostatnia jest potrzebna w społeczeństwie zarówno na płaszczyźnie prywatnej, jak i w sektorze publicznym (Giddens, 2000).

Przedsiębiorstwa są podmiotami otwartymi – nieustannie dokonują wymiany z otoczeniem. Jest ona jednak dużo szersza niż zwykła przemiana czynników produkcji w gotowe dobra. Według Z. Zioło (2006) firmy przyczyniają się do poprawy jakości życia ich pracowników, prowadząc do polepszenia sytuacji całych gospodarstw domowych. Przez dalszą transmisję środków finansowych wpływają pozytywnie na wzrost gospodarczy w kontekście lokalnym, krajowym oraz ponadnarodowym (Zioło, 2006). Inni badacze wskazują również na pozytywny wpływ firm na obszary zastojowe i niedorozwinięte – wytwarzane dobra i generowany popyt na pracę prowadzą do podnoszenia się upadłych gospodarek (Littunen, 2000).

Połączenie firm z lokalnym otoczeniem ma jednak charakter dwustronny – wybór miejsca działania bardzo silnie wpływa na potencjalne możliwości rozwoju, ale także na kwestię przetrwania firmy (Storey, Wynarczyk, 1996; Littunen, 2000). W literaturze występuje kilka nurtów teoretycznych dotyczących decyzji lokalizacyjnych w przedsiębiorstwach.

Według nich na decyzję o ulokowaniu firmy wpływają dwa rodzaje czynników: powiązane z kosztami i popytem oraz z kwestią konkurencji (Combes, Overman, 2004). Ceny i dostępność czynników produkcji różnią się w zależności od miejsca ich pozyskania. Centrum przyciąga przedsiębiorstwa łatwą dostępnością do dostawców i klientów. Nurt ekonomii miejskiej zwraca również uwagę na występujące w dużych aglomeracjach korzystne efekty zewnętrzne, powodowane wzmożoną wymianą wiedzy i łatwiejszym dostępem do dóbr publicznych (Duranton, Puga, 2004). Ulokowanie na peryferiach pozwala zaś uniknąć konkurencji – zarówno w kontekście dostarczanego produktu, jak i na rynku czynników produkcji – te same środki można więc otrzymać po niższych cenach (Ottaviano, Thisse, 2004).

Na polepszenie warunków dla przedsiębiorstw w znaczący sposób może wpłynąć odpowiednio prowadzona polityka lokalna (Audretsch, Thurik, 2000). Poprzez ulgi podatkowe, sprzyjające regulacje prawne i przygotowanie instytucjonalne sektor publiczny może oddziaływać na dostępne dla firm warunki, zwiększać prawdopodobieństwo ich przetrwania oraz zachęcać do lokowania się w wyznaczonych regionach (Holtz-Eakin, 2000). Dodatkowo, skuteczna polityka może wpłynąć na kierunkowanie bodźców ekonomicznych – zmuszając firmy do zachowania prospołecznego i proekologicznego (Holtz-Eakin, 2000).

Jak pokazano wcześniej, działalność firm ma pozytywny wpływ na lokalną gospodarkę (Giddens, 2000; Holtz-Eakin, 2000; Littunen, 2000). W literaturze wykazano również, że wspieranie przedsiębiorczości ma bezpośrednie przełożenie na osiągnięcie celów typowych dla polityki rozwoju regionalnego: zwiększenie zatrudnienia, promowanie innowacyjności i poprawę warunków życia (Van Dijk, Pellenbarg, 2000; Zioło, 2006). Jest to szczególnie istotny aspekt w kontekście dążenia do spójności. Centra ze swojej natury mają wiele czynników atrakcyjnych dla przedsiębiorców. Władze obszarów peryferyjnych powinny zaś szczególnie koncentrować się na przyciąganiu przedsiębiorczości i tworzeniu preferencyjnych warunków do ich egzystencji – potencjał rozwojowy danego regionu zależy bowiem silnie od firm znajdujących się na jego terenie. Literatura dowodzi skuteczności polityki spójności w kierunku przyciągania inwestycji i biznesu (Bastile et al., 2008).

Europejskie podejście do spójności w polskich strategiach rozwoju regionalnego

Pojęcie spójności (cohesion)

Oprócz klasycznych teorii rozwoju regionalnego na kształtowanie europejskiej polityki regionalnej mocno oddziaływała również idea spójności (Blom-Hansen, 2005). Nie ma ona jednoznacznej definicji, a samo pojęcie cohesion ewoluowało w czasie (Greta, 2014). W kontekście polityki regionalnej „spójność” po raz pierwszy pojawiła się w dyrektywie UE z 1986 r. i jej poziom był mierzony jako PKB w relacji do średniej w UE (Barry i Begg, 2003). Miała ona wyrażać relatywny stopień rozwoju krajów członkowskich. Na jej podstawie określano obszary, które powinny zostać objęte pomocą finansową. Obecnie spójność można zdefiniować jako dążenie do niwelowania nierówności w różnych obszarach życia, takich jak: możliwości wykształcenia i zatrudnienia, dochody, stan środowiska naturalnego, szanse i wyniki (Begg, 2003; Blom-Hansen, 2005; Molle, 2007; McCann i Ortega-Argilés, 2011).

Spójność może być rozpatrywana na dwóch płaszczyznach – spójności wewnętrznej (jednostkowej), którą można uzyskać poprzez promowanie dynamicznego rozwoju biedniejszych regionów, do uzyskania jednolitej stopy wzrostu w ramach jednego kraju; oraz spójności europejskiej (całościowej), która koncentruje się na różnicach między krajami członkowskimi (Begg, 2003; Greta, Tomczak-Woźniak, 2014). Druga płaszczyzna stanowi podstawę do budowania strategii konwergencyjnych, jest powiązana z decyzjami o włączeniu kraju do strefy euro oraz wpływa na ogólny kierunek przepływu europejskich funduszy pomocowych (McCann, Ortega-Argilés, 2011). Spójność jednostkowa zaś jest fundamentem do kształtowania szczegółowych polityk terytorialnych wewnątrz kraju (Blom-Hansen, 2005).

Pojęcie spójności często dzieli się na trzy nurty: spójność ekonomiczną, społeczną i terytorialną (Barry i Begg, 2003; Greta, Tomczak-Woźniak, 2014). W tej pierwszej zwraca się uwagę na wyrównywanie rozwoju gospodarczego między regionami oraz dążenie do równomiernego poziomu aktywności ekonomicznej (Molle, 2005; Greta, Tomczak-Woźniak, 2014). Spójność społeczna koncentruje się na aspekcie równego dostępu do edukacji i rynku pracy oraz dbałości o dobrobyt wszystkich grup ludności (Gradstein, Justman, 2002; Greta, Tomczak-Woźniak, 2014). Aspekt terytorialny wyraża się zaś następująco: nikt nie powinien mieć ograniczonych możliwości rozwoju ze względu na miejsce pracy czy zamieszkania (Davoudi, 2005; Molle, 2005; Greta, Tomczak-Woźniak, 2014).

Przegląd strategii rozwoju regionalnego w Polsce w kontekście spójności

Po transformacji systemowej polski rząd musiał poradzić sobie z dwoma głównymi problemami: zapewnieniem stabilności politycznej i gospodarczej. Oba te elementy znalazły swoje odzwierciedlenie w dążeniu do jak najszybszego przystąpienia do Unii Europejskiej (Bański, 2008). Choć finalne włączenie w struktury unijne nastąpiło dopiero w 2004 roku, wydarzenie to poprzedziły wieloletnie przygotowania. Oprócz ujednolicenia systemu prawnego i przybliżenia instytucjonalnego ważnym wyzwaniem było przeprowadzenie skutecznej reformy terytorialnej (Gilowska et al., 1998).

Reorganizacja podziału administracyjnego była niezbędna, aby utworzyć silne regiony, które mogłyby konkurować w skali europejskiej (Gilowska et al., 1998; Gorzelak, 2002). Utworzona została sieć 16 miast wojewódzkich, mających tworzyć lokomotywy wzrostu dla otaczających je obszarów. Niżej w hierarchii znalazły się powiaty, a następnie gminy. Trójstopniowy podział terytorialny, oparty na większej autonomii oraz możliwości samostanowienia o budżecie i polityce lokalnej, miał wspierać dążenia do zrównoważonego rozwoju (Gorzelak, 2002). Taka organizacja miała również ułatwić skuteczną redystrybucję funduszy europejskich (Herbut et al., 2007).

Unia Europejska jest jednym z głównych źródeł finansowania projektów rozwoju regionalnego w Polsce (Gilowska et al., 1998). Siłą rzeczy, kierunki i sposoby kształtowania polityki terytorialnej w kraju opierają się bardzo silnie na dyrektywach europejskich. Również strategie okresu przedakcesyjnego, w którym starano się jak najbardziej zbliżyć krajowe warunki życia do standardów unijnych, były mocno inspirowane planami zachodnimi (Gilowska et al., 1998). Zgodnie więc z podejściem europejskim, w centrum polskiej polityki rozwoju regionalnego od lat 90. ubiegłego wieku stawiano spójność.

Poniżej znajduje się krótki przegląd polskich planów rozwoju regionalnego. Przedstawiłam w nim również środki ukierunkowane na osiąganie spójności, zgodnie z metodologią zawartą w kolejnych edycjach Europejskiej Strategii Zrównoważonego Rozwoju.

1994–1999 – koncentracja na infrastrukturze i przekształceniu instytucjonalnym poprzez przygotowanie do przeprowadzenia reformy terytorialnej, dążenie do decentralizacji polityk rozwojowych (Gilowska et al., 1998); większy nacisk położony na podnoszenie ogólnej konkurencyjności poszczególnych regionów (Gorzelak i Jałowiecki, 2001) niż na dążenie do spójności między nimi; brak aktywnej polityki terytorialnej ze względu na przeświadczenie o niekorzystnym jej wpływie na wolnorynkową konkurencję i deficyt wykształconych narzędzi wsparcia lokalnego (Szlachta, 2011),

2000–2006 – początki budowy skutecznej polityki regionalnej w Polsce, opartej na strategiach europejskich (Szlachta, 2011); dążenie do spójności terytorialnej poprzez rozwój i modernizację infrastruktury transportowej oraz wzmacnianie powiązań peryferii z metropoliami (Gorzelak, 2002); szczególna koncentracja na harmonizacji rozwoju wewnątrz kraju poprzez wsparcie regionów zapóźnionych i zagrożonych marginalizacją (Szlachta, 2011); dążenie do spójności europejskiej poprzez pobudzanie innowacji oraz budowę kanałów ich transmisji, a także inwestowanie w kapitał ludzki (Gorzelak, 2002),

2007–2013 – zwiększenie autonomii i odpowiedzialności regionów w zakresie dysponowania funduszami spójności jako odpowiedź na brak „jednolitej recepty rozwojowej” (Fésüs, Roller, 2011); w kontekście spójności terytorialnej nadal ważnym elementem pozostało inwestowanie w obszary najsłabiej rozwinięte, m.in. poprzez rozwój infrastruktury (Jankowska, 2005), jednak równocześnie nastąpiło wyraźne przeniesienie akcentu na inwestycje niematerialne, związane ze spójnością ekonomiczną, np. poprzez rozwój kapitału ludzkiego, promowanie innowacji i gospodarności, dostosowywanie przedsiębiorstw do zmiennych warunków rynkowych i przystosowywanie pracowników do nowych miejsc pracy (Jankowska, 2005;
Fésüs, Roller, 2011),

2014–2020 strategia „Europa 2020” – przesunięcie priorytetu z dążenia do spójności – na wzrost inteligentny (Strzelecki, 2011; Szlachta, 2011); koncentracja na indywidualnych potrzebach regionów; odkrywanie i wspieranie indywidualnej ścieżki rozwojowej danego terytorium; akcent na specjalizację regionalną i naturalny potencjał obszaru (Strzelecki, 2011); odejście od przestrzennego aspektu prowadzenia polityki i pominięcie aspektu dyfuzji rozwoju na rzecz silniejszej walki o konkurencyjność państwa jako całości (Szlachta, 2011).

Rodzina modeli interakcji przestrzennych

Klasyczne modele interakcji przestrzennych pozwalają na prześledzenie wzorców przemieszania i przepływów między obszarami z wykorzystaniem narzędzi ekonometrycznych. Ich zastosowania są bardzo szerokie: od modelowania zachowań jednostek w przestrzeni, przez odkrywanie wzorców migracyjnych, aż po wyznaczanie optymalnego rozmieszczenia ośrodków użyteczności publicznej (lotniska, centra handlowe, szkoły wyższe itp.) (Fotheringham, O’Kelly, 1989).

Rodzinę modeli interakcji przestrzennych można przedstawić następująco:

gdzie T oznacza modelowany przepływ między obszarami i oraz j, v przedstawia siłę napędową przepływu z miejsca i (propulsiveness), zaś w oznacza siłę przyciągania do miejsca j (attractiveness). W modelu znajduje się również czynnik c, oznaczający separację przestrzenną między i oraz j (spatial separation). Parametry μ, α oraz β są wyznaczane w wyniku kalibracji modelu i oznaczają siłę oddziaływania danej zmiennej zależnej (Fotheringham, O’Kelly, 1989).

Naturalnie, odpowiednią formę modelu dobiera się ze względu na specyfikę badanego zjawiska. Popularne jest nakładanie ograniczeń na parametry μ i/lub α (Fotheringham, O’Kelly, 1989). Ważne jest również dopasowanie odpowiedniej formy funkcyjnej do każdego z czynników. Jest to szczególnie istotne dla zmiennej związanej z separacją przestrzenną – dobranie formy wykładniczej, potęgowej lub wielomianowej wpływa na wyniki estymacji (Taylor, O’Kelly, 1975).

Dzięki swojej elastycznej formie modele interakcji przestrzennych znajdują szerokie zastosowanie w literaturze. Używa się ich podczas badań nad migracją (LeSage, Pace, 2008), systemami transportu (Rodrigue, 2016), zależnościami handlowymi (Burger et al., 2009) czy wyceną nieruchomości (Can, 1990). Mogą też służyć do modelowania optymalnego rozmieszczenia centrów użyteczności publicznej (Hodgson, 1990; Harris, Batty, 1993). Znane są również zastosowania w kierunku modelowania procesów dyfuzji innowacji (Oldenburg, Glanz, 2008; Rogers, 2010).

Badanie empiryczne zasięgu wpływu centrum na peryferie

To badanie empiryczne ma wykryć obszar objęty dyfuzją bodźców ekonomicznych płynących z centrum na peryferie. Przeprowadzona analiza dynamiczna dla lat 1996–2017 ma pomóc w ocenie strategii rozwoju regionalnego. Przeprowadzone badanie na poziomie gminnym ma być podstawą do oceny działań dotyczących spójności prowadzonych w Polsce.

Badania spójności w literaturze

Ze względu na brak ścisłej definicji spójności nie ma jednoznacznej metodyki oceny efektów polityki regionalnej (López et al., 2008). Badacze najczęściej koncentrują się na konkretnym elemencie strategii. Szacują wtedy wpływ stosowanych narzędzi politycznych na eliminację dotychczasowych nierówności i rozwarstwień w danym sektorze (López et al., 2008). Ocena empiryczna jest najczęściej przeprowadzana za pomocą metod binarnych, takich jak regresja nieciągła (RDD) (Pellegrini et al., 2013). Prowadzi się również badania „dostępności”, oceniające wpływ infrastruktury na poprawę komunikacji między obszarami (López et al., 2008).

Na polskim podwórku oceną dyfuzji rozwoju z centrów na peryferie zajmowali się Herbst i Wójcik (2013). Używali miar korelacji przestrzennej, by wyznaczyć gminy objęte wpływem miast wojewódzkich. Podobne badanie, ale już z wykorzystaniem modeli interakcji przestrzennych, przeprowadziła Kopczewska (2013). W swoim artykule oceniała odległość, w której wpływ metropolii wygasa (w kontekście spadku dochodów i wydatków inwestycyjnych czy wzrostu bezrobocia na peryferiach).

Wykorzystany model teoretyczny

Wzorując się na badaniach dyfuzji obecnych w literaturze (Oldenburg, Glanz, 2008; Kopczewska, 2013) oraz koncepcji teoretycznej Fotheringhama (1989) wykorzystany został model interakcji przestrzennych z podwójnym ograniczeniem:

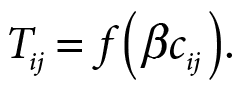
Parametr separacji przestrzennej 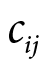przedstawia odległość dzielącą obiekty i oraz j, podlegające interakcji. W celu odwzorowania nieliniowego wzrostu kosztu ekonomicznego wraz z oddalaniem się od centrum – wykorzystano wielomianową formę funkcyjną.

Chociaż lokalne warunki rozwoju zależą od wielu czynników, nie zostały wprowadzone dodatkowe zmienne objaśniające. Jest to duże uproszczenie, ale jest ono wprowadzone świadomie z dwóch powodów. Po pierwsze, głównym celem badania jest określenie zasięgu obszaru metropolitalnego i prześledzenie zmian jego wielkości, po drugie zaś – dzięki temu zwiększają się możliwości interpretacyjne modelu, przy zachowaniu jego porównywalności między kolejnymi okresami. Jest to zresztą podejście zgodne z literaturą (López et al., 2008; Herbst, Wójcik, 2013).

Wykorzystany model – zgodnie z uznanymi teoriami rozwoju terytorialnego – odwzorowuje przepływy jednostronne (impulsy z centrum do peryferii). Jedyną modyfikacją jest uwzględnienie współzależności między sąsiadującymi gminami (wynikającej m.in. z przynależności do tych samych powiatów). Zmiana ta została dokonana poprzez dodanie opóźnienia przestrzennego w błędzie modelu.

Model teoretyczny z uwzględnieniem powyższych modyfikacji wygląda następująco:

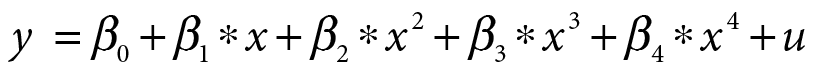
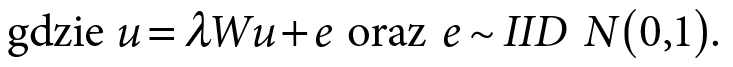
Modelowany przepływ 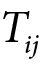będzie odzwierciedlał dyfuzję bodźców gospodarczych ze stolicy województwa do obszaru peryferyjnego. Intensywność zjawiska y w regionie zależy od względnej lokalizacji regionu, określonej odległością x regionu od centrum. Niestety, wyznaczenie jednego wskaźnika ekonomicznego, który mógłby przedstawić wzrost i potencjał oraz odwzorować sytuację rynkową regionu, jest niezwykle trudne. Jednak, jak wykazano wcześniej, istnieje bardzo wysokie powiązanie między stanem lokalnej gospodarki a działającymi na jej obszarze firmami (Giddens, 2000; Holtz-Eakin, 2000; Littunen, 2000). Opierając się na tej logice oraz na korzystnym sprzężeniu zwrotnym polityki rozwojowej i działalności przedsiębiorstw (Van Dijk, Pellenbarg, 2000; Zioło, 2006), jako miarę poziomu „korzystnych bodźców gospodarczych” na danym obszarze przyjęto wskaźnik przedsiębiorczości, rozumiany jako liczba firm per capita, w relacji do średniej krajowej.

W wyniku estymacji otrzymamy równanie będące wielomianem odległości. Po stronie zmiennej objaśniającej będą kolejne poziomy przedsiębiorczości, przedstawione jako procent średniej krajowej. Bardzo istotnym elementem będzie przecięcie wielomianu z poziomem 100%. Będzie to oznaczało granicę wpływu centrum na rozwój danego regionu (Kopczewska, 2013). Dzięki prostej konstrukcji modelu, promień obszaru metropolitalnego będzie można wyznaczyć z dokładnością do jednego kilometra.

Warto również zwrócić uwagę na parametr λ. Stanowi on miarę podobieństwa sąsiedzkiego (Kopczewska, 2011). Jeśli wynosi zero – autokorelacja przestrzenna między lokalizacjami sąsiedzkimi nie zachodzi. Odpowiednio, im jest wyższy – tym bardziej są podobne do siebie okoliczne rejony. Istotna zależność przestrzenna błędu oznacza również, że sąsiedzi będą w podobny sposób reagować na dotykające ich szoki. Ponadto, wystąpienie ich na jednym obszarze wpłynie na kolejne (Kopczewska, 2011). W tej interpretacji im wyższy parametr lambda, tym większa podatności gmin na przekazywanie między sobą impulsów rozwojowych i silniejsza między nimi siła dyfuzji (Kopczewska, 2011).

Kolejnym ważnym elementem w interpretacji modelu jest zmiana powyższych charakterystyk w czasie – po zestawieniu wyników z kolejnych lat będziemy w stanie stwierdzić, czy granica obszarów metropolitalnych przesunęła się oraz czy sąsiadujące gminy zbliżają się do siebie, czy raczej zachodzi proces autonomizacji.

Metody oceny modelu

Do oceny modelu przestrzennego wykorzystuje się dwa podstawowe kryteria informacyjne. Pierwszym z nich jest miara SRMSE (standardized root mean ­squared error). Według Fotheringhama (1989) jest to najlepszy wskaźnik informacyjny dla modeli interakcji przestrzennych (w tym lepszy niż R2). Jego wzór prezentuje się następująco:

gdzie n oznacza liczbę, T oznacza macierz przepływów, T’ jej oszacowanie, a zapis ij wyznacza kolejny element danej macierzy.

Miara ta zwykle przyjmuje wartości z zakresu (0–1) i przedstawia poziom uchwycenia zależności przestrzennych w modelu. Jego interpretacja jest następująca: wartości mniejsze niż 0,5 oznaczają bardzo dobre dopasowanie; statystka zbliżona do poziomu 0,75 oznacza, że udało się uchwycić główne trendy. SRMSE powyżej jedności pojawia się stosunkowo rzadko i sugeruje bardzo słabe dopasowanie przestrzenne modelu (Fotheringham, O’Kelly, 1989).

Drugim, ważnym kryterium informacyjnym, jest miara Akaike (AIC). Sposób jego wyliczania przedstawiono poniżej:

gdzie 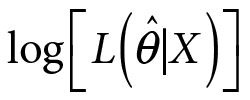oznacza logarytm funkcji estymatora najwyższej wiarygodności dla podanych danych, p przedstawia wymiar parametru θ. Pierwszy człon interpretuje się jako miara niedopasowania modelu, drugi zawiera karę za zwiększanie liczby parametrów modelu (Lee, Ghosh, 2009).

Przy porównywaniu dwóch modeli poszukuje się jak najniższej wartości tego wskaźnika (Bozdogan, 1987). Wewnątrz jednego – porównuje się wyliczoną miarę dla modelu liniowego (linear) oraz przestrzennego (spatial). Jeśli druga wartość jest niższa – zastosowany model przestrzenny lepiej odwzorowuje zależności występujące w danych (Kopczewska, 2011).

Szczegóły badania

Badanie zostało przeprowadzone na danych gmin – są one autonomicznymi jednostkami, odbierającymi impulsy ekonomiczne z wyższych w hierarchii obszarów (powiatów i województw). Są na tyle niewielkie w skali kraju, że pozwalają prześledzić lokalne trendy i wyznaczyć promień obszaru objętego dyfuzją z dobrą dokładnością. Jednocześnie stanowią one agregaty, dla których można odnaleźć łatwo dostępne dane opisujące realną sytuację ekonomiczną. Warto w tym miejscu również wspomnieć o roli gmin w świetle zasady subsydiarności (Kęska, 2007). Według tej reguły, stojącej u podstaw metodyki prowadzenia polityki regionalnej w Polsce, właśnie w najniższych jednostkach samorządowych powinno znajdować się najwięcej kompetencji i mocy decyzyjnej, gdyż najpełniej potrafią one odpowiadać na specyficzne potrzeby lokalnej społeczności. Wyższe jednostki mają służyć pomocą jedynie w projektach, które przekraczają możliwości gmin (Kęska, 2007).

Za zmienną objaśnianą przyjęta została liczba przedsiębiorstw w gminie per capita, wyrażona jako procent średniej krajowej. Jest to statystyka, która w dobry sposób przybliża poziom przedsiębiorczości w regionie. Zestaw zmiennych objaśniających tworzą kolejne potęgi wyrażonej w kilometrach odległości gminy od stolicy województwa (jako punkt referencyjny przyjęto centrum miasta oraz geograficzny środek jednostki terytorialnej).

Finalnie oszacowano następujący model:

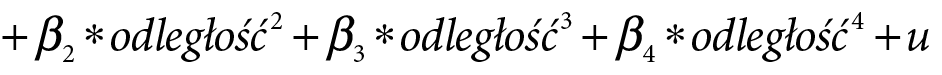
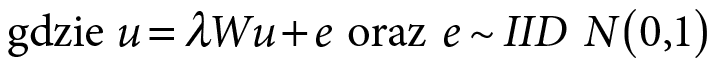
Regresję przeprowadzono dla danych BDL GUS z lat 1996–2017. Analiza statystyczna dla najświeższego okresu ma za zadanie przedstawić wpływ centrum wojewódzkiego na poziom rozwoju w otaczających je gminach – będzie pomocna do odkrycia wzorca i będzie stanowiła punkt odniesienia dla dalszych badań. Analiza dynamiczna dla dwóch poprzednich dekad pozwoli prześledzić zmiany zasięgu obszaru metropolitalnego. Dzięki niej uda się ocenić, czy stosowane do tej pory strategie rozwoju regionalnego się sprawdziły i czy doprowadziły do zwiększenia spójności terytorialnej w Polsce. Pozwoli również odpowiedzieć na pytanie, jak duża jest skala zjawiska peryferyjności oraz w jakim stopniu gminy są otwarte na zjawisko dyfuzji.

Wyniki modelu

Wyniki analizy w ujęciu statystycznym przedstawia tabela 1. Wszystkie parametry modelu oraz lambda są istotne statystycznie na poziomie 1%. Wskaźnik podobieństwa sąsiedzkiego jest wysoki, co sugeruje dużą zdolność do dyfuzji między okolicznymi regionami (wynosi aż 0,635). Wartość Akaike dla wariantu przestrzennego jest niższa niż w przypadku liniowym – wybrana forma jest więc zgodna z zależnościami terytorialnymi. Wartość SRMSE dla tak oszacowanego modelu wyniosła 0,3400246. Oznacza to dobre dopasowanie modelu do trendów przestrzennych.

Jak wskazano, zmienna objaśniana została wyrażona jako procent średniej krajowej. Oznacza to, że wartości powyżej jedności (100%) wyznaczają przestrzeń ponadprzeciętnego rozwoju (miejsc objętych dyfuzją rozwoju z centrum). Ten newralgiczny punkt najłatwiej dostrzec na wykresie dopasowanego wielomianu (por. rysunek 1).

Co jest widoczne na wykresie, wraz ze wzrostem odległości od centrum wojewódzkiego wartość zmiennej objaśnianej spada. Co więcej, już dla wartości 38 km wielomian przecina od góry wartość średniej krajowej. Później poziom przedsiębiorczości pozostaje poniżej przeciętnej (z niewielkim odchyleniem o 5% w okolicach 100 km od centrum).

Tabela 1. Wyniki oszacowania modelu dla danych z roku 2017

	Oszacowanie	Błąd standardowy	z value	Pr (>|z|)
Stała	1.8871e+00	8.8469e-02	21.3305	< 2.2e-16
odległość	–4.6140e-2	5.6501e-03	–8.1663	2.220e-16
odległość2	7.8726e-04	1.3021e-04	6.0462	1.483e-09
odległość3	–5.3803e-6	1.1885e-06	–4.5272	5.977e-06
odległość4	1.2637e-08	3.6650e-09	3.4481	0.0005645
Testy oraz λ	Lambda	SRMSE	Akaike (spatial)	Akaike (linear)
	0.63543***	0,34002	1915.4	2625.1

*** istotność na poziomie 0,01

Źródło: opracowanie własne.

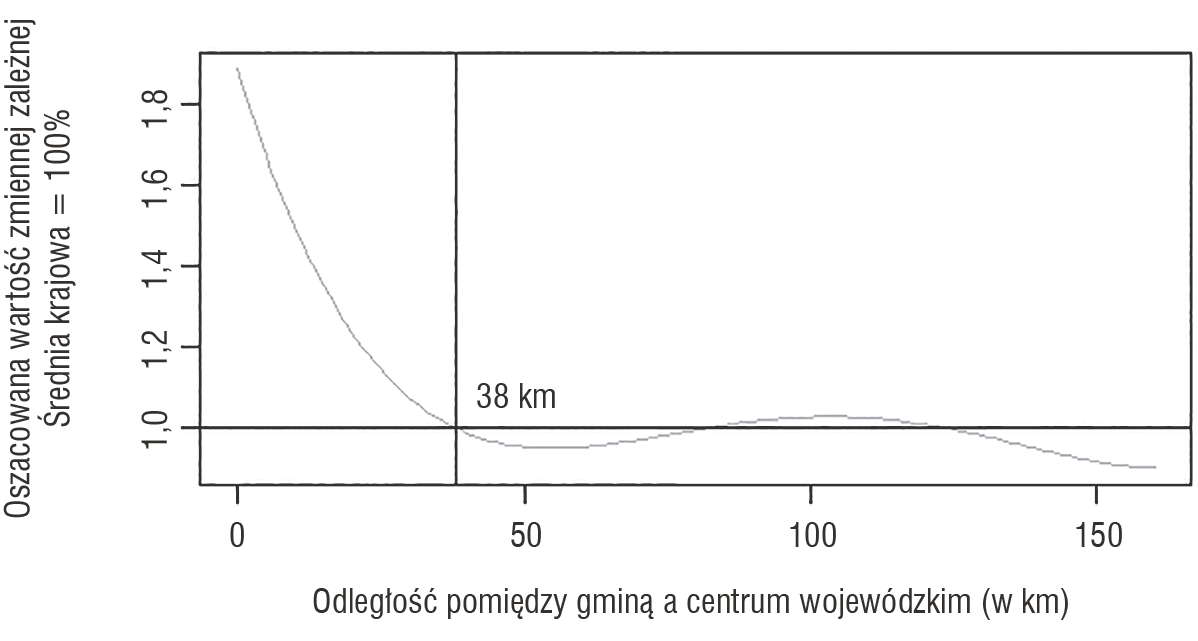
Rysunek 1. Wielomian odległości jako zmienna objaśniająca (dane z 2017 r.)

Źródło: opracowanie własne przy pomocy programu R.

Wynikają z tego następujące wnioski: wraz z oddalaniem się od centrum poziom rozwoju znacząco spada – w dalej położonych gminach jest on poniżej średniej. Występowanie obszaru z ponadprzeciętnymi wartościami zmiennej objaśnianej potwierdza istnienie terenów metropolitalnych – czerpiących z pozytywnego wpływu centrum, wyraźnie odróżniających się od dalszych regionów. Jednak ich zasięg jest niewielki – w promieniu 38 km wpływ wojewódzkiego „motoru wzrostu” całkowicie wygasa.

Warto przyjrzeć się tej wielkości na tle przeciętnego oddalenia gmin od ośrodków wojewódzkich – średnia odległość tych jednostek od centrów wynosi 30–80 km, w zależności od regionu. Co ważne, ponad 71% gmin jest położonych dalej niż 40 km od stolicy województwa (por. tabela 4 w aneksie). Skala zjawiska peryferyjności jest więc niepokojąco wysoka. Przy wzięciu pod uwagę głównej strategii niwelowania różnic rozwojowych, a więc systemu transmisji bodźców z silnych centrów do obszarów peryferyjnych, okaże się, że w 2017 r. z tego planu korzyści czerpała zaledwie jedna czwarta gmin (25,73% jednostek terytorialnych w promieniu co najwyżej 38 km od centrum województwa).

Aby przekonać się, czy otrzymany wynik jest spójny z tendencjami historycznymi i czy rzeczywiście może rzutować na całościową ocenę skuteczności strategii rozwojowych w Polsce, przeliczono powyższy model również na danych z lat 1996–2016.

Wizualna prezentacja wyników potwierdza zaobserwowany wzorzec zachowania funkcji dla ostatnich dwudziestu lat (por. rysunek 2). Dla każdego okresu wykres przecina od góry linię 100% w odległości około 40 km. Oznacza to, że występuje wyraźny podział na gminy objęte oddziaływaniem centrów wojewódzkich oraz obszary peryferyjne o przeciętnym (a także poniżej przeciętnym) poziomie gospodarczym. Ponownie można zaobserwować niewielki wzrost rozwoju w okolicach 100 km od centrum – jednak nadal nie jest on zbyt silny (w granicach 7%). Szczegółowe oszacowania modeli i wyniki testów diagnostycznych znajdują się w tabeli 7 w aneksie.

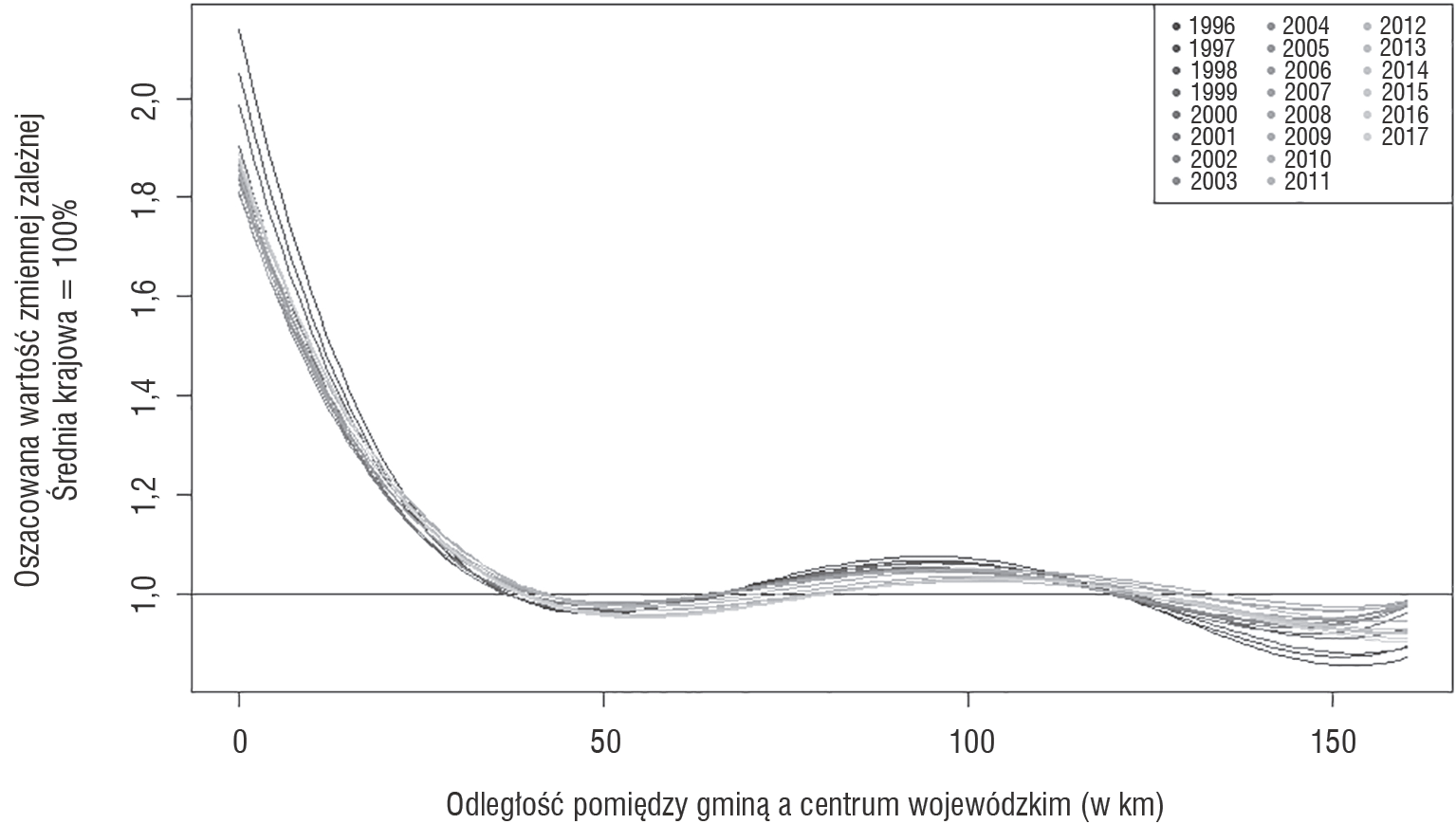
Rysunek 2. Wielomian odległości jako zmienna objaśniająca (dane 1996–2017)

Źródło: opracowanie własne przy pomocy programu R.

Ciekawe są również zmiany punktu przecięcia wielomianu z osią OY, czyli wielkości oszacowanej w modelu stałej. Są to punkty określające wysokość badanej cechy w centrach. Dla lat najwcześniejszych (1996–1999: ciemnoszare, prawie czarne linie) wykres rozpoczyna się najwyżej. Oznacza to wysoki stopień rozwarstwienia między centrum a resztą województwa (wartości cechy w okolicach 200% średniej). W kolejnych latach nierówności malały. Zagęszczenie (średnio) szarych linii w rekordowo niskim punkcie 1,8 oznacza zmniejszenie dysproporcji o 20 punktów procentowych w ciągu dziesięciolecia (szczególnie niskie wartości dla roku 2008). Jest to korzystna informacja z punktu widzenia dążenia do spójności. Można jednak zauważyć, że w ostatnich latach tendencja się odwróciła – najjaśniejsze linie znajdują się wyżej. Nie udało się więc trwale zredukować nierówności między centrum a peryferiami – dla roku 2017 poziom przedsiębiorczości w stolicach wojewódzkich wyniósł 189% średniej krajowej, a więc dziewięć p.p. wyżej niż dekadę wcześniej (por. tabela 7 w aneksie). W ostatnim czasie zaszedł więc proces dywergencyjny.

Analiza danych dla ostatnich lat wykazała ograniczenie przestrzenne dyfuzji rozwoju z miast na peryferie. Warto jednak przyjrzeć się, jak zmieniała się ta granica rok do roku; jaki był jej trend – rosnący, malejący czy zupełnie niewyraźny? Wydzielenie przestrzeni analizy na kolejne podokresy nowych rozwiązań strategicznych pozwoli określić, jak dane plany wpływały na osiąganie spójności.

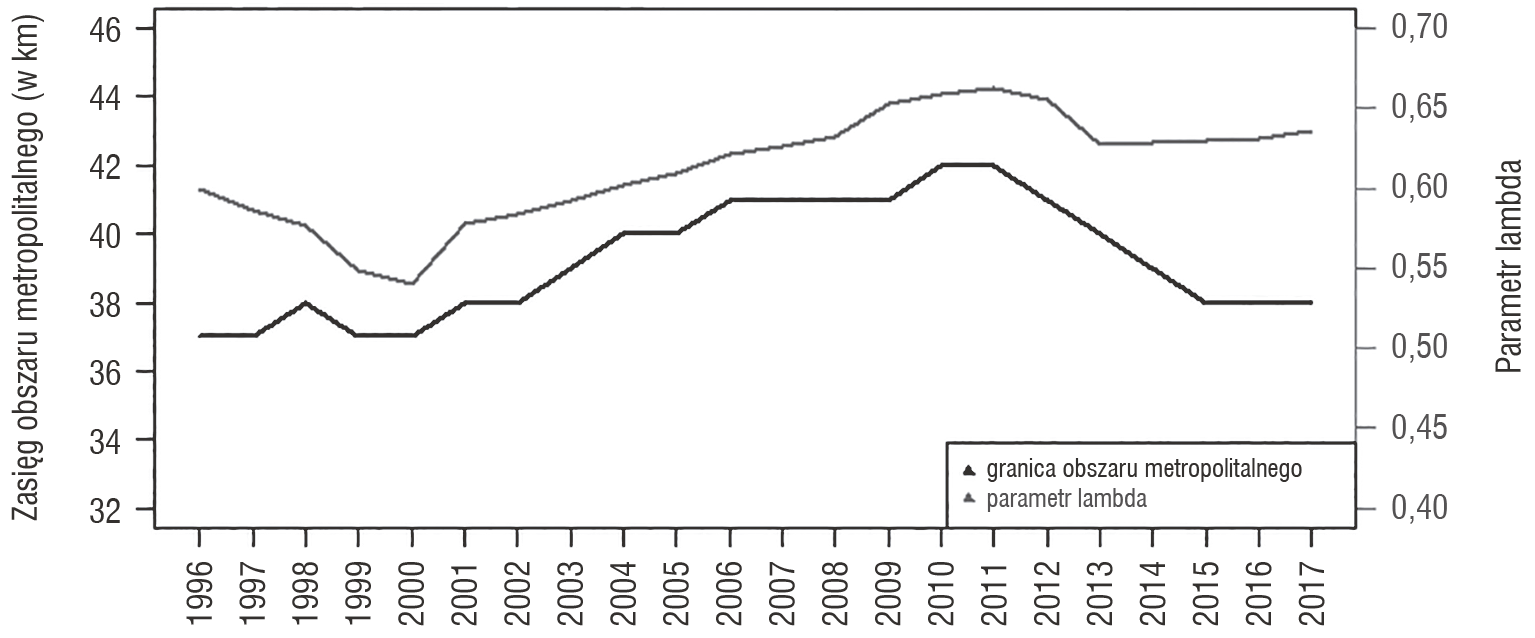
Rysunek 3. Dynamika zmian promienia obszarów metropolitalnych oraz parametru podobieństwa sąsiedzkiego

Źródło: opracowanie własne przy pomocy programu R.

Kolejny wykres przedstawia zmiany promienia obszarów metropolitalnych (por. rysunek 3). Pokazano na nim również przekształcenia parametru podobieństwa sąsiedzkiego lambda.

Na podstawie analizy wykresu można stwierdzić, że aż do roku 2011 zasięg obszarów metropolitalnych się poszerzał. W ciągu piętnastu lat udało się zwiększyć ich promień o 5 km. W skali całego kraju oznacza to istotną zmianę. W promieniu 37 km od centrum wojewódzkiego znajduje się jedynie 23% gmin. Przesunięcie granicy do 42 km oznacza, że dyfuzją objęte jest już 31% jednostek lokalnych (por. tabela 5 w aneksie). Niestety, po tym czasie tendencja się odwróciła i obszar metropolitalny szybko się skurczył. Spadek był tak silny, że w roku 2017 zasięg centrum wynosi tyle samo, co dwie dekady wcześniej – zaledwie 38 km (por. tabela 3 w aneksie).

Warto również zwrócić uwagę na zmiany wielkości parametru λ – ich dynamika jest w większej części spójna ze wzorcem zmian promienia odległości. W latach 1996–2000 gminy oddalały się od siebie. Mogło to mieć związek z przeprowadzanymi reformami (szczególnie reformą terytorialną), które miały na celu zwiększenie autonomiczności zarządzania na szczeblu lokalnym. W nowym stuleciu, aż do roku 2011, obserwuje się zaś znaczący wzrost λ. Gminy były coraz bardziej otwarte na dyfuzję, a równocześnie obszar metropolitalny się zwiększał. Później trend się odwrócił i do końca trwania tego planu rozwojowego (rok 2013) parametr podobieństwa sąsiedzkiego malał. Lata 2014–2017 przyniosły jednak pewną niespodziankę. Rozpoczęto wtedy wdrażanie nowego modelu polityki smart. Choć wpływ centrów wojewódzkich nadal się zmniejszał, parametr λ zaczął stopniowo wzrastać. Okoliczne gminy ponownie zaczęły się do siebie zbliżać i bardziej otwierać na lokalne procesy dyfuzyjne. Równocześnie działanie centralnych lokomotyw rozwoju straciło na znaczeniu, a zjawisko peryferyjności się powiększyło.

Obserwacja rezultatów kolejnych edycji strategii rozwojowych prowadzi do następujących wniosków: aż do roku 2000 polska polityka regionalna nie prowadziła do większych sukcesów. Kolejne lata przypadające na strategię, w której centrum stała spójność ekonomiczna pozwoliły na zmniejszenie obszaru peryferyjnego oraz na większe otwarcie gmin na procesy dyfuzyjne. Wpływ polityki lat 2007–2013 pozostaje niejasny – bowiem aż do roku 2011 można było zaobserwować dalsze wzmacnianie spójności i poszerzanie obszarów rozwiniętych. Później jednak ten efekt wygasł i aż do końca obserwowanego okresu wpływ lokomotyw wzrostu spadał. Być może przygotowywano się już wtedy do nowego paradygmatu spójności, która miała mniej zależeć od centralnych nakazów, a bardziej od autonomicznych potrzeb lokalnego otoczenia. Po roku 2014, kiedy rozpoczęto wdrażanie programu Europa 2020, opartego na modelu smart, zjawisko peryferyjności nadal rosło – można więc powiedzieć, że centralny system transmisji innowacji był wadliwy. Mimo to, w ciągu ostatnich lat udało się nieznacznie otworzyć gminy na komunikację ze swoimi sąsiadami i bardziej na regionalne zjawiska transmisji.

Metoda L-momentów i skośności

Dążenie do spójności można również badać statystycznie poprzez porównanie rozkładu danej cechy w różnych punktach w czasie (Kopczewska, 2014). Już prosta obserwacja wykresów gęstości pozwala określić, czy dana własność stała się bardziej równomiernie rozdysponowana (konwergencja), czy mocniej skoncentrowała się w centrum (dywergencja) (por. rysunek 4). Trzecią możliwością jest przesunięcie globalne, czyli poprawa sytuacji wszystkich jednostek, bez przesunięć w rozkładzie danej cechy między podmiotami (Kopczewska, 2014).

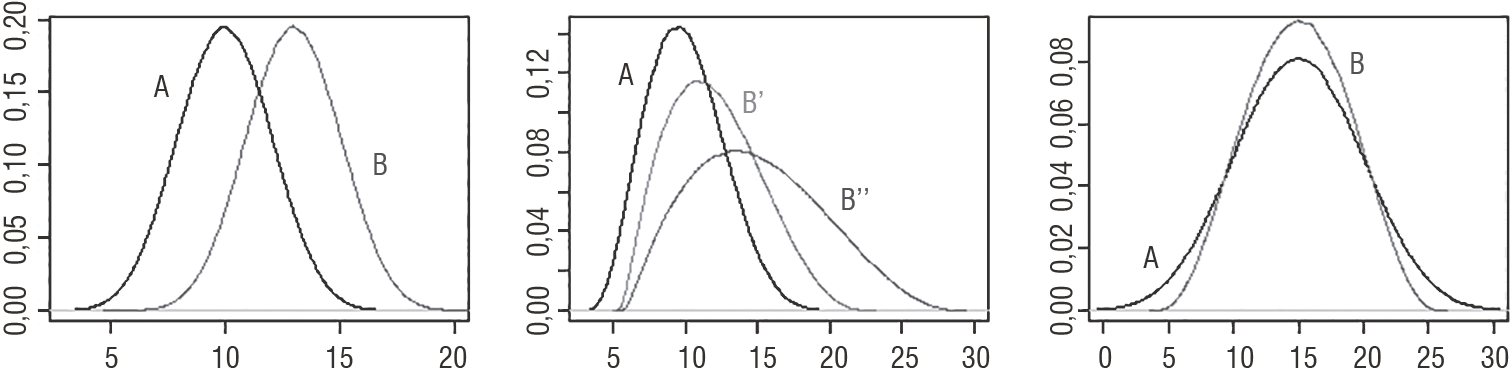
Rysunek 4. Przesunięcia rozkładów teoretycznych cechy w różnych scenariuszach rozwoju (zmiana z A do B); (a) przesunięcie globalne, (b) dywergencja, (c) wzrost spójności (konwergencja)

Źródło: opracowanie własne przy pomocy programu R, na podstawie Kopczewska (2014).

Rysunek 5. Zmiany rozkładu cechy z okresu t na okres t+1 w różnych scenariuszach rozwoju; (a) przesunięcie globalne, (b) dywergencja, (c) wzrost spójności (konwergencja)

Źródło: opracowanie własne przy pomocy programu R, na podstawie Kopczewska (2014).

Podobne informacje można odczytać z wykresów rozrzutu – porównuje się na nich wartości danej cechy w okresie t oraz t+1 i sprawdza, jak kształtuje się położenie punktów względem osi 45o (Kopczewska, 2014). Zmiana w kierunku spójności przedstawia się tam jako szybszy wzrost jednostek o niższych wartościach (ponad prostą) i słabszy przyrost wyższych (pod prostą). Dywergencja jest przedstawiona jako szybsze odsuwanie się wartości największych. Zmiana globalna może być wykryta jako równoległe przesunięcie wszystkich punktów powyżej linii 45o (por. rysunek 5).

Tych samych informacji, w bardziej obiektywny sposób, może również dostarczyć analiza momentów centralnych rozkładu2. Porównywanie własności danych do charakterystyk rozkładów teoretycznych jest typową metodą statystyczną, pozwalającą na analityczne określenie zachowania zjawiska.

Zmiany wielkości momentów centralnych w czasie można w prosty sposób przetłumaczyć na przesunięcia w stronę spójności (zmniejszenie różnic między maksymalną i minimalną wartością), dywergencji (zwiększenie koncentracji i powiększenie nierówności) lub też zmiany globalnej (przesunięcie całego wykresu). Kierunki zmian momentów centralnych typowe dla powyższych wzorców konwergencyjnych przedstawia tabela 2.

Tabela 2. Zmiany statystyk rozkładu pod wpływem konwergencji, dywergencji i zmiany globalnej

Zmiana	Centralna tendencja	Wariancja	Skośność	Kurtoza
Przesunięcie globalne	Rosnąca	Bez zmian	Bez zmian	Bez zmian
Konwergencja	Bez zmian	Malejąca	Malejąca	Rosnąca
Dywergencja	Rosnąca	Rosnąca	Rosnąca	Malejąca

Źródło: opracowanie własne na podstawie Kopczewska (2014).

Niestety, wyznaczanie estymatorów momentów centralnych na podstawie danych empirycznych w wielu przypadkach jest utrudnione. Przy dużej liczbie obserwacji odstających (typowej dla naturalnych zjawisk) pojawia się istotny błąd oszacowania. Ponadto, porównywanie wyższych momentów dla rozkładów o różnych właściwościach jest właściwie niemożliwe, a literatura na ten temat jest niewystarczająca (Kopczewska, 2014). Można jednak zastosować przekształcenia liniowe – L-momenty (Hosking, 1990; Kopczewska, 2014). Dostarczają tych samych informacji, co zwykłe momenty centralne, jednak ich zachowanie jest lepsze z kilku powodów: są jednak bardziej odporne na obserwacje odstające, mało liczne próbki i brak symetrii danych (Hosking, 1990), można je przeliczyć dla większej liczby rozkładów (Hosking, 1990). Dodatkowo, ich wartości są ograniczone do przedziału (0,1), dzięki czemu można je łatwiej porównywać między rodzinami rozkładów.

Kolejne L-momenty są wyznaczane według poniższego wzoru:

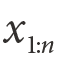gdzie r oznacza numer porządkowy kolejnego momentu (np. 1: L-średnia, 3: L-skoś­ność), n przedstawia wielkość próby, a  oznacza i-tą statystykę pozycyjną rozkładu (według zasady: ≤ ≤ … ≤ ) (Elamir, Seheult, 2003).

Zgodnie z przedstawionym wyżej podejściem, w celu dokonania analizy zmian konwergencyjnych w Polsce w analizowanym okresie (1996–2017), przeliczono podstawowe momenty centralne (średnią i odchylenie standardowe) oraz L-skośność i L-kurtozę dla liczby przedsiębiorstw w gminie per capita. Dynamika zmian otrzymanych statystyk jest przedstawiona na rysunku 6. Dokładne wartości parametrów znajdują się w tabeli 6 (w aneksie).

Na podstawie otrzymanych danych można wyznaczyć cztery podokresy analizy o różnych charakterystykach. W danych z lat 1996–2000 obserwuje się wzrost średniej i odchylenia standardowego z równoczesnymi niewielkimi zmianami trzeciego i czwartego momentu centralnego. Takie zmiany sugerują przesunięcie globalne – niewiele zmieniło się w kontekście spójności, nastąpiła zaś wyraźna poprawa konkurencyjności całego obszaru. W latach 2000–2007 można dostrzec silniejszy spadek L-skośności, przy utrzymaniu w miarę stałej kurtozy i niewielkim wzroście pierwiastka wariancji. To przekształcenie też ma cechy przesunięcia globalnego, ale jest połączone z przemianą konwergencyjną – obserwujemy przesunięcie środka rozkładu nieco w prawo, co oznacza poprawę sytuacji jednostek średnich. Dane z lat 2007–2011 stanowią niemal modelowy przykład zwiększania spójności – skoś­ność spada, kurtoza rośnie, a zmiany średniej i odchylenia standardowego nie są zbyt dynamiczne. Jednak dane z okresu 2011–2017 opowiadają zgoła inną historię – do 2013 r. obserwujemy proces dywergencyjny, a później następuje względna stabilizacja wszystkich parametrów, za wyjątkiem rosnącej średniej. Osiągnięta przed rokiem 2011 spójność się cofa. Późniejszy wzrost wartości przeciętnej można wytłumaczyć silniejszym rozwojem punktów odstających o szczególnie wysokich wartościach – wzrastają więc centra, a sytuacja peryferii się nie poprawia.

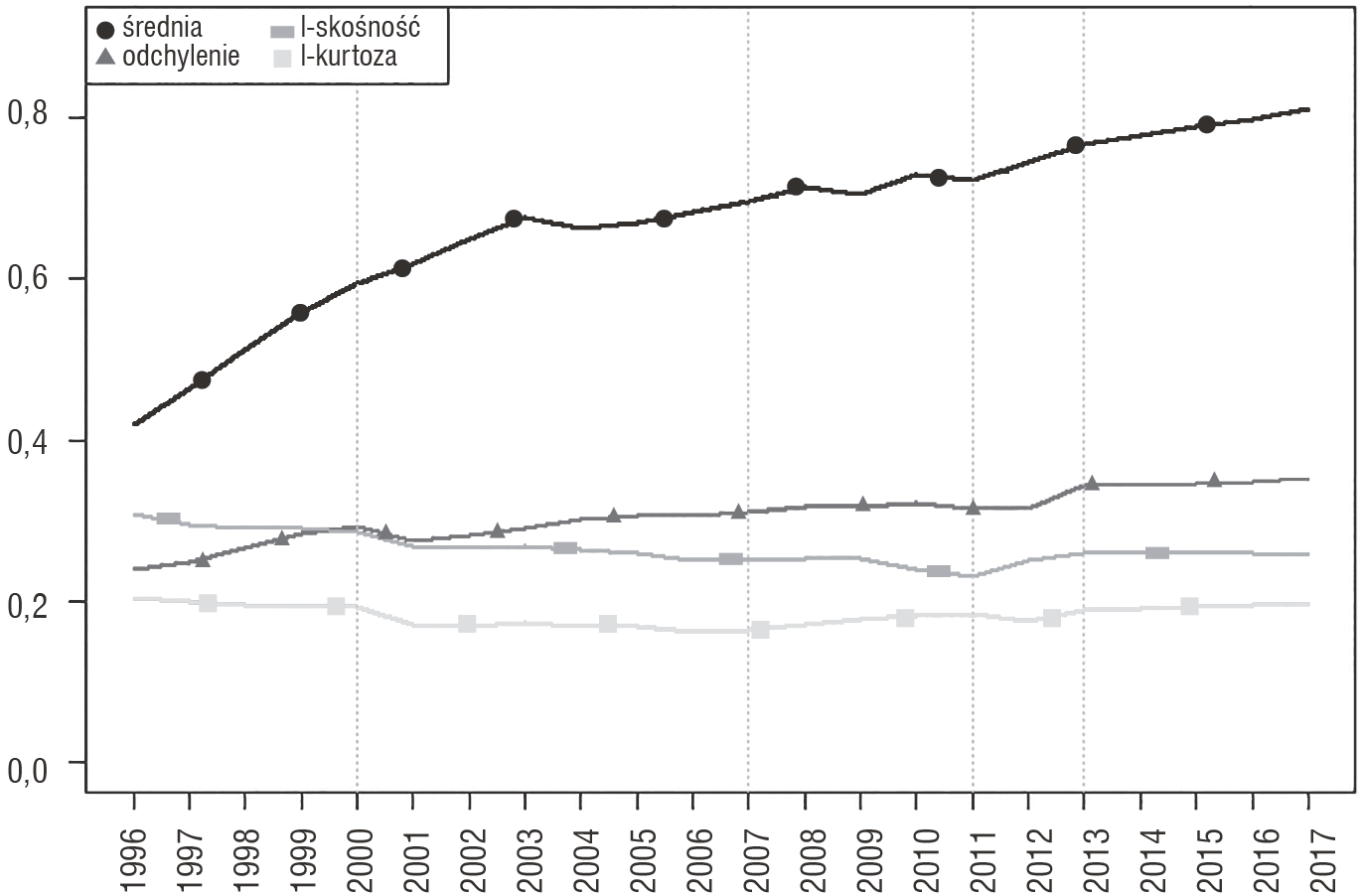
Rysunek 6. Zmiany statystyk i L-momentów rozkładu liczby przedsiębiorstw per capita (*10)3 w gminach w latach 1996–2017

Źródło: opracowanie własne przy pomocy programu R.

Potwierdzenie powyższych obserwacji znajdziemy w analizie rozkładów z okresu t na okres t+1 (por. rysunek 7). Wykres dla lat 1996–2000 przedstawia przesunięcie globalne – niemal wszystkie punkty przesunęły się ponad oś 45 stopni. W górnej partii rysunku widać również kilka obserwacji odstających – są to dynamicznie rozwijające się centra o wysokich i szybko rosnących wartościach badanej cechy. Dane z lat 2000–2007 również wskazują na przesunięcie globalne, jednak najmocniej dotknęło ono punkty środkowe (poprawa sytuacji obszarów przeciętnych). Kolejny wykres wykazuje wzorzec konwergencyjny w danych: wartości niższe i średnie przesunęły się powyżej krzywej, a obserwacje odstające znalazły się poniżej osi 45 stopni. Powiększyła się więc spójność – udało się zniwelować rozwarstwienie między centrum a peryferiami. Dane z lat 2011–2017 nie wykazują już podobnego zachowania – rozkład cechy w niższych i średnich obszarach nie zmienił się znacząco. Zamiast tego można dostrzec przesunięcie obserwacji wyższych i najmocniej odstających powyżej linii 45 stopni. Nierówności między obszarami się zwiększyły, a wzrost w tym okresie dotyczył jedynie rozwijających się centrów i regionów o wyższym potencjale.

Rysunek 7. Przesunięcia rozkładów w czasie z okresu t do t+1; (a) 1996–2000,
(b) 2000–2007, (c) 2007–2011, (d) 2011–2017

Źródło: opracowanie własne przy pomocy programu R.

***

Polityka skierowana na zrównoważony i inteligentny rozwój miała za zadanie wspierać naturalny potencjał regionów oraz pobudzać do wzrostu obszary o słabszym potencjale. Efektem skutecznych strategii rozwojowych powinien być więc wyrównany poziom przedsiębiorczości w skali kraju. Jak wynika z badań empirycznych, strategia inwestowania w centra się nie sprawdza. W ciągu ostatnich 20 lat nie udało się trwale zwiększyć terenów metropolitalnych (objętych pozytywnym wpływem centrum). Wręcz przeciwnie, w ostatnich latach promień wyznaczający obszar objęty dyfuzją się zmniejszył. Pomimo rosnących wydatków przeznaczanych na niwelowanie nierówności nie widać znacznej poprawy spójności międzyregionalnej. Trend wskazujący na dynamicznie rozwijające się centra i wydrenowane peryferie jest nadal silny. Co więcej, w ostatniej dekadzie polaryzacja między tymi obszarami się pogłębiła.

Wyniki otrzymane za pomocą analizy L-momentów są spójne z poprzednim badaniem. Międzyokresowe przekształcenia rozkładów potwierdziły, że na okres 2007–2011 przypadają największe sukcesy w zakresie zwiększania spójności, chociaż poprawa sytuacji obszarów najmniej rozwiniętych była widoczna już od roku 2000. Po tym czasie tendencja się odwróciła – wyraźny wzrost konkurencyjności można dostrzec jedynie w centrach i wyżej rozwiniętych regionach.

Wcześniejsze badania potwierdzają uzyskane obserwacje – Kopczewska (2013) oraz Herbst i Wójcik (2013) również wskazywali na występowanie silnych trendów polaryzacyjnych w polskiej gospodarce. Co więcej, malejący z biegiem lat wskaźnik SRMSE pokazuje coraz lepsze dopasowanie przestrzenne modelu. Oznacza to, że odległość ma decydujący wpływ na dostępne w regionie szanse rozwojowe.

Czy można więc powiedzieć, że dotychczasowa polityka regionalna się nie sprawdziła? W jednych aspektach się nie sprawdziła, w innych tak. Między innymi dzięki wsparciu funduszy strategicznych Polska i inne kraje Europy Środkowo-Wschodniej wykazały wysoki stopień konwergencji do poziomu Unii Europejskiej (Repacki, 2014; Batóg, 2010). Średnio Polska dąży więc do spójności całościowej. Jednak cel jednostkowy nie został osiągnięty – nadal występuje bardzo silny podział na bardziej i mniej rozwinięte obszary wewnątrz kraju. Jest on widoczny zarówno w skali wojewódzkiej (Camagani, Capello, 2013), jak i gminnej.

Oddalenie terytorialne od centrum zdaje się obecnie stanowić główną barierę dla przedsiębiorczości i wzrostu. Dotychczasowy model inwestowania w „motory rozwoju” jest więc nietrafiony. Proces dyfuzji jest istotnie zaburzony przez bariery komunikacyjne, co sprawia, że niektóre obszary czerpią z obecnego modelu nieproporcjonalnie mniej niż inne.

Warto również zwrócić uwagę na moment odwrócenia się tendencji poszerzania obszarów metropolitalnych – był to czas wygasania planów rozwojowych, opartych na wspieraniu infrastruktury i dofinansowywaniu obszarów szczególnie zapóźnionych. W następnych latach zwrócono się w stronę idei wzrostu inteligentnego. Być może to nowe podejście do prowadzenia polityki regionalnej nie sprawdziło się w polskich realiach. Bardziej złożony model teoretyczny smart nie został dobrze zaadaptowany, a jego działanie nie zostało odpowiednio dopasowane do potrzeb regionów. Prawdziwe może być też stwierdzenie, że polska siatka dyfuzyjna jest jeszcze za słabo rozwinięta, aby móc skorzystać z tak pomyślanego modelu wzrostu. Bliższe zbadanie tej kwestii pozostanie jednak obszarem do dalszych badań.

Bibliografia

Acemoglu, D. (2012). Introduction to economic growth. Journal of Economic Theory, 147.2: 545– 550.

Audretsch, D. B., Thurik, A. R. (2000). Capitalism and democracy in the 21st century: from the managed to the entrepreneurial economy. Journal of Evolutionary Economics, 10.1–2: 17–34.

Azariadis, C. Drazen, A. (1990). Threshold externalities in economic development. The Quarterly Journal of Economics, 105.2: 501–526.

Bański, J. (2008). Polska i Europa Środkowo-Wschodnia w koncepcjach podziału Europy. Problematyka geopolityczna ziem polskich. Warszawa: Instytut Gospodarki i Przestrzennego Zagospodarowania PAN.

Barry, F. Begg, I. (2003). EMU and cohesion: introduction. JCMS: Journal of Common Market Studies, 41.5: 781–796.

Batóg, J. (2010). Konwergencja dochodowa w krajach Unii Europejskiej: analiza ekonometryczna. Rozprawy i Studia/Uniwersytet Szczeciński, 780.

Begg, I. (2003). Complementing EMU: rethinking cohesion policy. Oxford Review of Economic Policy, 19.1: 161–179.

Blom-Hansen, J. (2005). Principals, agents, and the implementation of EU cohesion policy. Journal of European Public Policy, 12.4: 624–648.

Bozdogan, H. (1987). Model selection and Akaike’s information criterion (AIC): The general theory and its analytical extensions. Psychometrika, 52.3: 345–370.

Burger, M., Van Oort, F., Linders, G. (2009). On the specification of the gravity model of trade: zeros, excess zeros and zero-inflated estimation. Spatial Economic Analysis, 4.2: 167–190.

Camagni, R., Capello, R. (2013). Regional innovation patterns and the EU regional policy reform: Toward smart innovation policies. Growth and Change, 44.2: 355–389.

Can, A. (1990). The measurement of neighborhood dynamics in urban house prices. Economic Geography, 66.3: 254–272.

Capello, R., Kroll, H. (2016). From theory to practice in smart specialization strategy: emerging limits and possible future trajectories. European Planning Studies, 24.8: 1393–1406.

Cesarski, M. (2013). Infrastruktura osadnicza w gospodarce regionalnej–kwestie równoważenia rozwoju. Kwartalnik Kolegium Ekonomiczno-Społecznego. Studia i Prace, 3: 9–25.

Combes, P. Overman, H. (2004). The spatial distribution of economic activities in the European Union. Handbook of Regional and Urban Economics. Elsevier: 2845–2909.

Davoudi, S. (2005). Understanding territorial cohesion. Planning, Practice & Research, 20.4: 433– 441.

Duranton, G., Puga, D. (2004). Micro-foundations of urban agglomeration economies. Handbook of Regional and Urban Economics. Elsevier: 2063–2117.

Elamir, E., Seheult, A. (2003). Trimmed L-moments. Computational Statistics & Data Analysis, 43.3: 299–314.

Fésüs, G., Roller E. (2011). Zmiana paradygmatu w polityce spójności, w: Nowy paradygmat rozwoju–najnowsze trendy i perspektywy polityki regionalnej. Warszawa: Ministerstwo Rozwoju Regionalnego.

Foray, D. (2014). Smart specialisation: Opportunities and challenges for regional innovation policy. Routledge, 2014.

Foray, D., et al. (2013). The goals of smart specialisation. S3 Policy Brief Series, 1: S3.

Fotheringham, S., O’Kelly, M. (1989). Spatial interaction models: formulations and applications. Dordrecht: Kluwer Academic Publishers.

Friedmann, J. (1967). A general theory of polarized development. Santo Domingo: The Ford Foundation.

Fujita, M., Krugman, P., Venables, A. (2001). The spatial economy: Cities, regions, and international trade. MIT Press.

Giddens, A. (2000). The third way and its critics. London: Polity Press.

Gilowska, Z. et al. (1998). Kierunki polityki regionalnej Polski. Studia Regionalne i Lokalne, 24 (57).

Glasmeier, A. (2000). Economic geography in practice: local economic development policy. The Oxford Handbook of Economic Geography, 200: 559–579.

Gorzelak, G. (2002). Polskie regiony w procesie integracji europejskiej. Studia Regionalne i Lokalne, 2–3 (9): 55–73.

Gorzelak, G., Jałowiecki, B. (2001). Strategie rozwoju regionalnego województw: próba oceny. Studia Regionalne i Lokalne, 1 (5): 41–59.

Gradstein, M., Justman, M. (2002). Education, social cohesion, and economic growth. American Economic Review, 92.4: 1192–1204.

Greta, M., Tomczak-Woźniak, E. (2014). Problem spójności w nowej polityce regionalnej UE na lata 2014–2020. Optimum. Studia Ekonomiczne, 4.

Grzeszczak, J. (1999). Bieguny wzrostu a formy przestrzeni spolaryzowanej. Warszawa: IGiPZ PAN.

Harris, B. Batty, M. (1993). Locational models, geographic information and planning support systems. Journal of Planning Education and Research, 12.3: 184–198.

Hausner, J. (2001). Modele polityki regionalnej w Polsce. Studia Regionalne i Lokalne, 1: 5–24.

Herbst, M., Wójcik, P. (2013). Delimitacja dyfuzji rozwoju z miast metropolitalnych z wykorzystaniem korelacji przestrzennej. Studia Regionalne i Lokalne, 4 (54): 5–21.

Herbut, R. et al. (2007). Wymiary polityki regionalnej w aspekcie politycznym, społecznym i gospodarczym. Legnica: Państwowa Wyższa Szkoła Zawodowa im. Witelona, seria Wspólnota Akademicka.

Hirschman, A. (1958). The strategy of economic development. New Haven–London: Yale University Press.

Hodgson, J. (1990). A flow‐capturing location‐allocation model. Geographical Analysis, 22.3: 270–279.

Holtz-Eakin, D. (2000). Public policy toward entrepreneurship. Small Business Economics, 15.4: 283–291.

Hooghe, L. et al. (red.) (1996). Cohesion policy and European integration: building multi-level governance. Oxford University Press on Demand.

Hosking, J. (1990). L‐moments: Analysis and estimation of distributions using linear combinations of order statistics. Journal of the Royal Statistical Society: Series B (Methodological), 52.1: 105–124.

Hryniewicz, J., Jałowiecki, B., Mync, A. (1997). Ruchliwość pracowników naukowych w latach 1994–1996. Studia Regionalne i Lokalne, 22 (55).

Jacobs J. (1969). Economy of cities. New York: Random House.

Jałowiecki, B., Gorzelak, G. (2004). Brain drain, brain gain, and mobility: Theories and prospective methods. Higher Education in Europe, 29.3: 299–308.

Jankowska, A. (2005). Fundusze Unii Europejskiej w okresie programowania 2007–2013. Warszawa: Polska Agencja Rozwoju Przedsiębiorczości.

Kęska, J. (2007). Zasada subsydiarności a samodzielność organizacyjna jednostek samorządu terytorialnego. Rocznik Żyrardowski, 5.

Kopczewska, K. (2011). Ekonometria i statystyka przestrzenna z wykorzystaniem programu
R CRAN. Warszawa: CeDeWu Wydawnictwa Fachowe.

Kopczewska, K. (2013). The spatial range of local governments: does geographical distance affect governance and public service? The Annals of Regional Science, 51.3: 793–810.

Kopczewska, K. (2014). L‐moments skewness and kurtosis as measures of regional convergence and cohesion. Statistica Neerlandica, 68.4: 251–266.

Lee, H., Ghosh, S. K. (2009). Performance of information criteria for spatial models. Journal of Statistical Computation and Simulation, 79.1: 93–106.

LeSage, J., Pace, K. (2008). Spatial econometric modeling of origin‐destination flows. Journal of Regional Science, 48.5: 941–967.

Lipshitz, G. (1992). Divergence versus convergence in regional development. Journal of Planning Literature, 7.2: 123–138.

Littunen, H. (2000). Networks and local environmental characteristics in the survival of new firms. Small Business Economics, 15.1: 59–71.

López, E., Gutiérrez, J., Gómez, G. (2008). Measuring regional cohesion effects of large-scale transport infrastructure investments: an accessibility approach. European Planning Studies, 16.2: 277–301.

Lucas, R. Jr. (1988). On the mechanics of economic development. Journal of Monetary Economics, 22.1: 3–42.

McCann, P., Ortega-Argilés, R. (2011). Smart specialisation, regional growth and applications to EU cohesion policy. EB Working Paper, 14.

Molle, W. (2007). European cohesion policy. Routledge.

Oldenburg, B., Glanz, K. (2008). Diffusion of innovations. Health Behavior and Health Education-Theory Research, and Practice, 313–330.

Ottaviano, G., Thisse, J. (2004). Agglomeration and economic geography. Handbook of Regional and Urban Economics. Elsevier: 2563–2608.

Pellegrini, G. et al. (2013). Measuring the effects of European Regional Policy on economic growth: A regression discontinuity approach. Papers in Regional Science, 92.1: 217–233.

Perroux, F. (1964). La economía del siglo XX. Barcelona: Ariel.

Pike, A., Rodríguez-Pose, A., Tomaney, J. (2016). Local and regional development. Routledge.

Rapacki, R., Próchniak, M. (2014). Wpływ członkostwa w Unii Europejskiej na wzrost gospodarczy i realną konwergencję krajów Europy Środkowo-Wschodniej. Ekonomia, 39: 87–122.

Rodrigue, J., Comtois, C., Slack, B. (2016). The geography of transport systems. Routledge.

Rogers, R. (2010). Diffusion of innovations. Simon and Schuster.

Rothschild, R. (1994). Adam Smith and the invisible hand. The American Economic Review, 84.2: 319–322.

Steyaert, C., Katz, J. (2004). Reclaiming the space of entrepreneurship in society: geographical, discursive and social dimensions. Entrepreneurship & Regional Development, 16.3: 179–196.

Strzelecki, Z. (2011). Strategiczne wyzwania Polski a polityka regionalna (wybrane problemy), w: Nowy paradygmat rozwoju–najnowsze trendy i perspektywy polityki regionalnej.

Szlachta, J. (2011). Strategiczne programowanie rozwoju regionalnego, w kierunku krajowego systemu myśli strategicznej w sferze polityki regionalnej, w: Nowy paradygmat rozwoju–najnowsze trendy i perspektywy polityki regionalnej.

Taylor, P., Openshaw, S. (1975). Distance decay in spatial interactions. Concepts and Techniques in Modern Geography.

Van Dijk, J., Pellenbarg, P. (2000). Spatial perspectives on firm demography. Papers in Regional Science, 79.2: 107–110.

Zioło, Z. (2006). Rola przedsiębiorczości w podnoszeniu konkurencyjności społeczeństwa i gospodarki. Przedsiębiorczość-Edukacja, 2: 10–17.

Aneks

Tabela 3. Sumaryczne zestawienie wyników empirycznej analizy dynamicznej

Rok	Przecięcie z 1 (km)	Ile procent gmin powyżej tej granicy	SRMSE	Lambda
1996	37	74,27	0,4638188	0.60006***
1997	37	74,27	0,4417460	0.58563***
1998	38	73,10	0,4291195	0.57692***
1999	37	74,27	0,4322264	0.54816***
2000	37	74,27	0,4213065	0.54075***
2001	38	73,10	0,3696147	0.57766***
2002	38	73,10	0,3593154	0.58415***
2003	39	71,81	0,3526909	0.59268***
2004	40	70,27	0,3693246	0.60141***
2005	40	70,27	0,3692844	0.60968***
2006	41	68,90	0,3597535	0.62131***
2007	41	68,90	0,3574328	0.62611***
2008	41	68,90	0,3516694	0.63196***
2009	41	68,90	0,3485856	0.65232***
2010	42	67,33	0,3378084	0.65903***
2011	42	67,33	0,3305196	0.66272***
2012	41	68,90	0,3199820	0.65547***
2013	40	70,27	0,3551768	0.62762***
2014	39	71,81	0,3486840	0.62824***
2015	38	73,10	0,3466401	0.62997***
2016	38	73,10	0,3449347	0.63055***
2017	38	73,10	0,3400246	0.63543***

Źródło: opracowanie własne przy pomocy programu R.

Tabela 4. Rozkład odległości gmin od centrum wojewódzkiego

Przedział odległości (km)	Częstość	Skumulowany odsetek gmin (%)
0–10	36	1,45
10–20	169	8,28
20–30	199	16,32
30–40	294	28,19
40–50	329	41,48
50–60	342	55,29
60–70	300	67,41
70–80	223	76,41
80–90	183	83,80
90–100	123	88,77
100–110	106	93,05
110–120	74	96,04
120–130	47	97,94
130–140	26	98,99
140–150	13	99,52
150–160	7	99,80
160–170	2	99,88
170–180	3	100,00

Źródło: opracowanie własne przy pomocy programu R.

Tabela 5. Rozkład odległości gmin od centrum wojewódzkiego w promieniu 35–45 km

Przedział odległości (km)	Skumulowany odsetek gmin w tych granicach (%) (w przeliczeniu na 2476 jednostek)
35–36	22,33
36–37	23,63
37–38	24,56
38–39	25,73
39–40	26,90
40–41	28,19
41–42	29,73
42–43	31,10
43–44	32,67
44–45	33,80

Źródło: opracowanie własne przy pomocy programu R.

Tabela 6. Momenty i L-momenty rozkładu liczby firm w gminie per capita (*10)

	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Średnia	0,419	0,464	0,512	0,558	0,594	0,617	0,649	0,676	0,662	0,670	0,682
Odchylenie	0,240	0,249	0,266	0,284	0,293	0,275	0,283	0,290	0,301	0,307	0,306
L-skośność	0,308	0,295	0,291	0,290	0,287	0,268	0,267	0,269	0,264	0,260	0,251
L-kurtoza	0,205	0,199	0,196	0,193	0,194	0,171	0,169	0,172	0,168	0,168	0,163
	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017
Średnia	0,696	0,714	0,704	0,729	0,721	0,745	0,766	0,778	0,789	0,796	0,810
Odchylenie	0,311	0,316	0,317	0,323	0,315	0,314	0,344	0,343	0,347	0,349	0,352
L-skośność	0,251	0,254	0,252	0,239	0,231	0,251	0,259	0,260	0,259	0,259	0,258
L-kurtoza	0,164	0,171	0,177	0,182	0,185	0,175	0,188	0,191	0,194	0,196	0,196

Źródło: opracowanie własne przy pomocy programu R.

Tabela 7. Szczegółowe wyniki estymacji modeli z lat 1996–2017

Rok	1996	1997	1998	1999	2000		2001	2002	2003	2004	2005	2006
Stała	2.138e+00***	2.050e+00***	1.985e+00***	1.904e+00***	1.865e+00***		1.858e+00***	1.836e+00***	1.812e+00***	1.854e+00***	1.857e+00***	1.843e+00***
Odległość	–6.436e-02***	–5.943e-02***	–5.513e-02***	–5.125e-02***	–4.929e-02***		–4.819e-02***	–4.660e-02***	–4.507e-02***	–4.650e-02***	–4.672e-02***	–4.542e-02***
Odległość^2	1.208e-03***	1.117e-03***	1.025e-03***	9.628e-04***	9.345e-04***		9.111e-04***	8.745e-04***	8.437e-04***	8.599e-04***	8.667e-04***	8.330e-04***
Odległość^3	–8.992e-06***	–8.333e-06***	–7.559e-06***	–7.167e-06***	–7.065e-06***		–6.896e-06***	–6.574e-06***	–6.331e-06***	–6.407e-06***	–6.483e-06***	–6.154e-06***
Odległość^4	2.278e-08***	2.119e-08***	1.902e-08***	1.822e-08***	1.829e-08***		1.794e-08***	1.701e-08***	1.634e-08***	1.646e-08***	1.674e-08***	1.570e-08***
Lambda	0.60006***	0.58563***	0.57692***	0.54816***	0.54075***		0.57766***	0.58415***	0.59268***	0.60141***	0.60968***	0.62131***
SL Sigma^2	0.21513	0.19514	0.18414	0.18682	0.1775		0.13662	0.12911	0.12439	0.1364	0.13637	0.12942
Akaike (spatial)	3425.3	3173.3	3023.6	3040.1	2908.7		2284.9	2149.5	2063.5	2298.1	2303.8	2183.4
Akaike (linear)	4047.1	3755.7	3587.2	3535.2	3385.2		2854.1	2733.3	2669.6	2938.6	2972.3	2877.5
SRMSE	0.4638188	0.441746	0.4291195	0.4322264	0.4213065		0.3696147	0.3593154	0.3526909	0.3693246	0.3692844	0.3597535

Rok	2007	2008	2009	2010	2011		2012	2013	2014	2015	2016	2017
Stała	1.828e+00***	1.804e+00***	1.828e+00***	1.847e+00***	1.863e+00***		1.871e+00***	1.873e+00***	1.872e+00***	1.878e+00***	1.889e+00***	1.887e+00***
Odległość	–4.447e-02***	–4.252e-02***	–4.279e-02***	–4.310e-02***	–4.320e-02***		–4.405e-02***	–4.487e-02***	–4.487e-02***	–4.550e-02***	–4.622e-02***	–4.614e-02***
Odległość^2	8.109e-04***	7.609e-04***	7.464e-04***	7.423e-04***	7.259e-04***		7.478e-04***	7.632e-04***	7.636e-04***	7.771e-04***	7.896e-04***	7.873e-04***
Odległość^3	–5.943e-06***	–5.470e-06***	–5.240e-06***	–5.187e-06***	–4.932e-06***		–5.144e-06***	–5.222e-06***	–5.230e-06***	–5.329e-06***	–5.412e-06***	–5.380e-06***
Odległość^4	1.502e-08***	1.359e-08***	1.276e-08***	1.262e-08***	1.161e-08**		1.225e-08***	1.233e-08**	1.238e-08***	1.260e-08***	1.277e-08***	1.264e-08***
Lambda	0.62611***	0.63196***	0.65232***	0.65903***	0.66272***		0.65547***	0.62762***	0.62824***	0.62997***	0.63055***	0.63543***
SL Sigma^2	0.12776	0.12367	0.12151	0.11411	0.10924		0.10239	0.12615	0.12158	0.12016	0.11898	0.11562
Akaike (spatial)	2155.1	2079.3	2052.7	1903	1798.3		1631.5	2125	2034.1	2006.4	1982.4	1915.4
Akaike (linear)	2860.9	2805.5	2863.2	2750.8	2659		2464.5	2812.1	2721.4	2697.6	2674.6	2625.1
SRMSE	0.3574328	0.3516694	0.3485856	0.3378084	0.3305196		0.319982	0.3551768	0.348684	0.3466401	0.3449347	0.3400246

Legenda: oznaczenia istotności 0.1, *0.05, **0.01, ***0.001

Źródło: opracowanie własne przy pomocy programu R.

---